引言
最近在网上冲浪的刷博客的时候, 看到一个题目.
总共有25匹马, 一共有5个赛道, 现在要选出跑的最快的5匹马, 至少需要比赛几次?
这个问题刚看到的时候, 看了一眼下面的答案就略过去了, 但是后面突然回想到这道题, 然后没有想通为什么是这样, 特此记录一下.
首先这个问题有一些潜在的限制, 例如没有计时器, 不然全跑一遍计时一次, 看成绩取top5就好了. 现在是每次只能跑5匹马, 知道这一轮的排序.
我们一步一步的来解决这个问题.
首先想如果将top5, 修改为top1. 需要怎么安排?
是不是可以将25匹马, 5匹一组跑一次, 每组选出跑的最快的一匹, 再跑一轮, 这一轮的第一名就是top1了.
当需要Top1时, 共需要5+1=6次
Ok, 到此我们先将上面的结果梳理一下, 将25匹马进行一下编号, 分为5组, 组编号为A,B,C,D,E, 组内的编号为1-5. 组内按照速度排序1-5, 每组按照顺序排序A-E
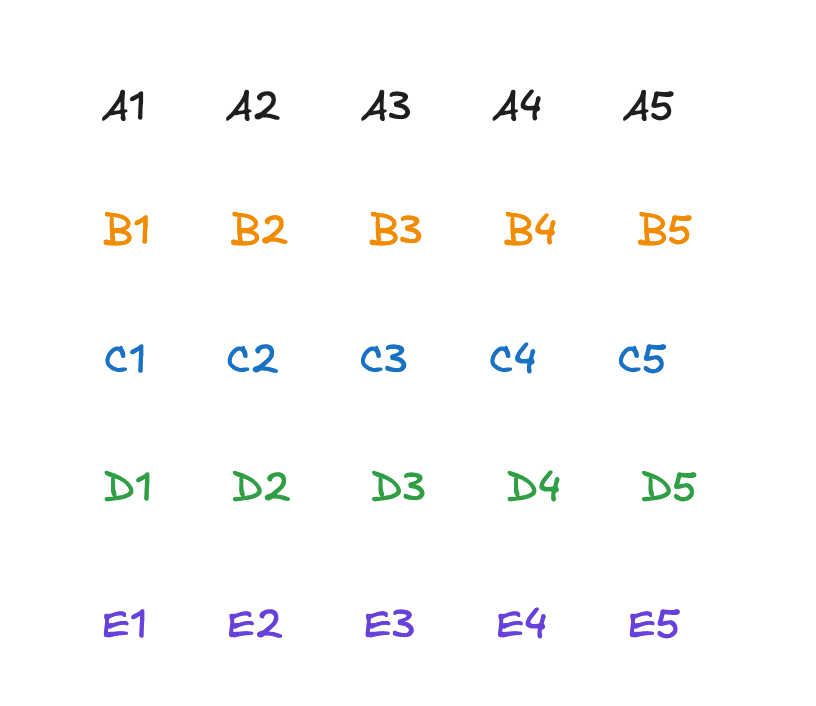
此时, A1>A2>A3>A4>A5, A1>B1>C1>D1>E1.
但是我们不能知道A2, B1的关系.
如果继续取top2, 需要怎么安排.
首先我们已经取出来了Top1. 那么剩下的人里面怎么取第二名呢.
最简单的方法是在跑一遍, 但是这样很明显的就会多跑.
我们现在已经有A1>A2>A3>A4>A5, A1>B1>C1>D1>E1. 这两个已知的排序.
是不是可以让A2, B1两匹马跑一次就可以得到谁是第二名了.
因为A2>A3, 如果A2<B1, 那么可证A3<B1.
当需要Top2时, 共需要6+1=7次
OK, 根据这个我们想一下, A2,B1是怎么找到的, 是不是从A1为起点, 查找走1步可以到达的节点.
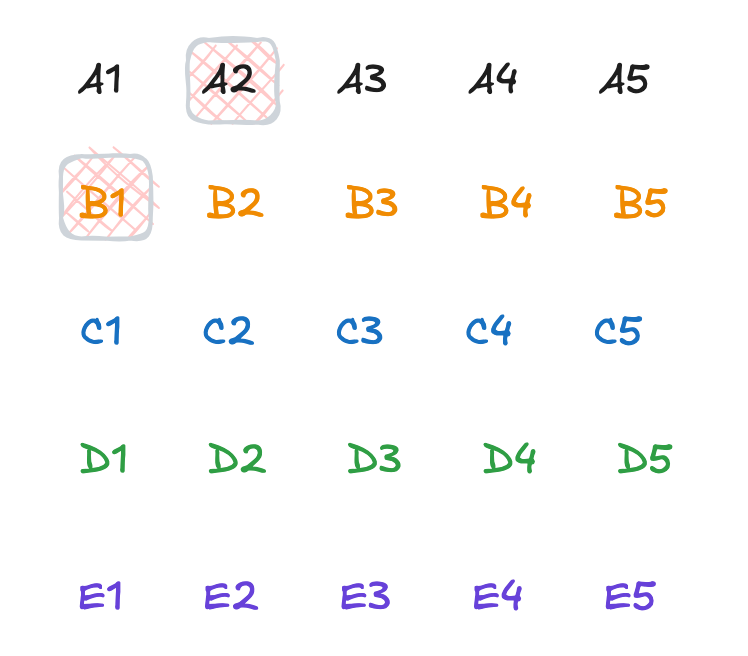
如果继续取Top3, 需要怎么安排.
假设我们已经让A2, B1跑了一轮, 得到他们两个之间的排名.
我们假设他们两个的第一名是A2. A2就是全局第二名.
此时全局第三要怎么找呢?
B2有资格参赛吗? 是不是没有资格, 因为前面还有B1. 所以仅需要B1和A3进行比赛就可以了.
同理如果B1得到第一名, 那么A3也没有资格参赛, 这时需要对C1, B2, A2进行比赛就可以了.
等一下, 这样的安排是最少的次数吗? 现在是争夺第二名的比赛中仅有两匹马, 争夺第三名有两匹或者三匹马比赛. 要找到前三, 需要在第二名的比赛后再额外比赛一次, 我们现在第二名和第三名的比赛要参加的马总数是4或者5, 没有超过5条赛道, 是不是可以合并成一次比赛决出2,3名?
我们从A1出发, 走2步, 所有可能到达的节点有:
A2, A3, B1, B2, C1
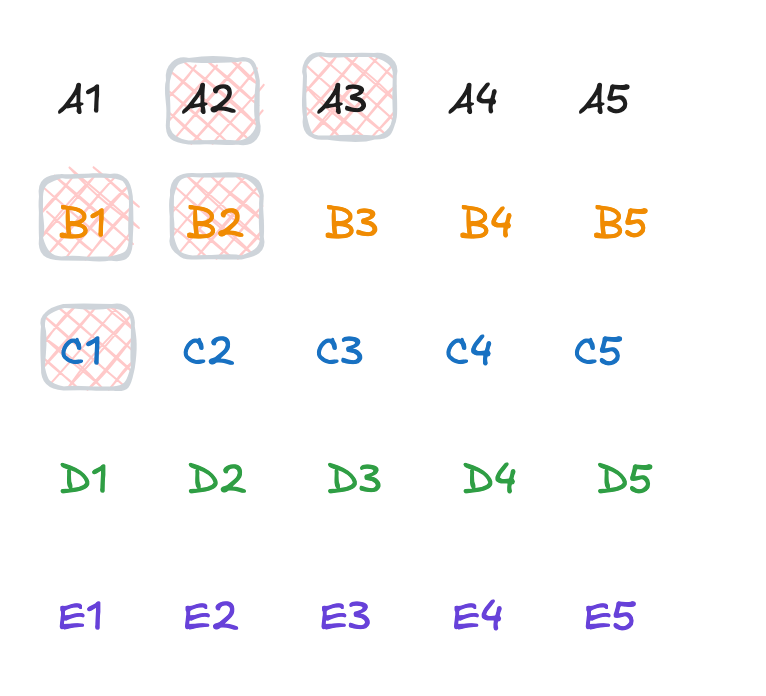
此时, 共有A2, A3, B1, B2, C1共5匹马, 而我们正好有5条赛道, 正好可以一次完赛.
这次完赛的第一,第二名, 正是我们全局的第二, 第三名. 可以自己证明一下.
当需要Top3时, 共需要6+1=7次
如果继续取Top4, 需要怎么安排.
我们首先按照之前的规律, 选出哪些马, 有资格争夺前四
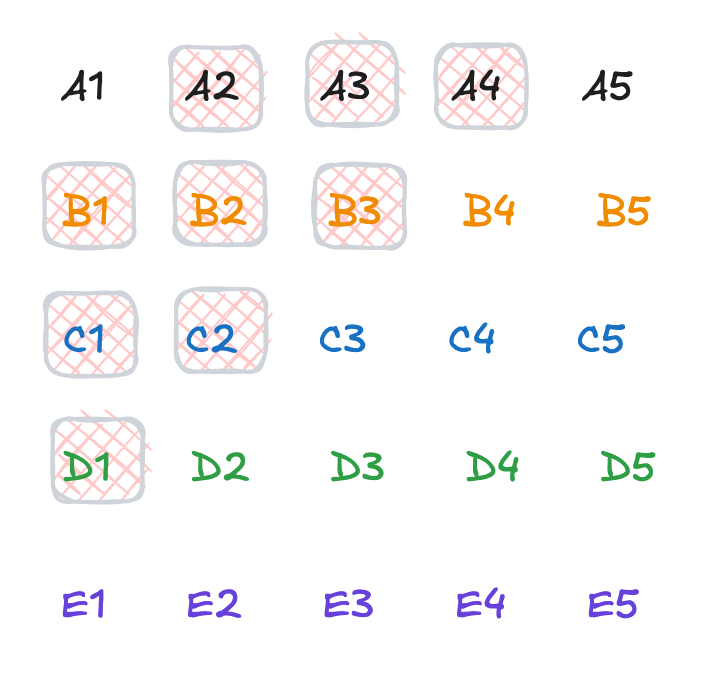
在Top3的比赛中, 共有5匹马进行比赛. A2, A3, B1, B2, C1. 完赛后, 我们就可以对他们之间再次进行排序.
这里面的第一,第二名名就是全局的第二,第三名.
这次比赛中的第三名, 能否作为全局的第四名呢?
这个是不可以的, 例如:
此次比赛A2>A3>B1. 我们能说B1是全局第四吗? 此时A4会不会比他快呢? 需要比赛一场才知道, 此时仅需要对B1, A4进行比赛即可.
我们根据上面的情况罗列一下第七轮比赛所有可能的结果:
-
A2, A3是第二, 第三名 此时争夺第四的资格只有
A4, B1两匹马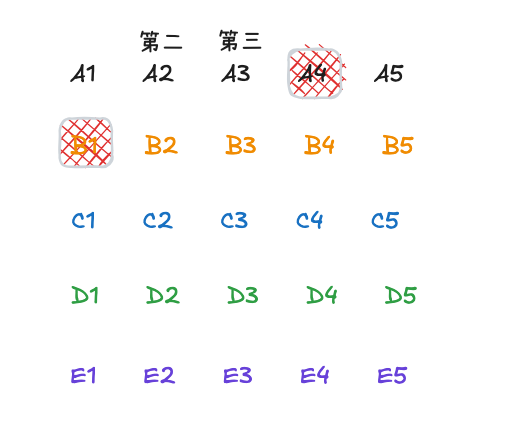
-
A2, B1是二三名 这时, 争夺第四资格的有
这时, 争夺第四资格的有A3,B2,C1三匹马. 而A3, B2, C1的排序我们在上一轮中, 就可以得到了. 所以这一轮就可以省略掉. 不需要进行比赛了 -
B1,B2是二三名
 这时, 争夺第四资格的有
这时, 争夺第四资格的有A2,B3,C1三匹马 -
B1, C2是二三名
这时, 争夺第四资格的有A2,B2,C2, D1四匹马
至此, 我们已经整理完成所有可能的情况, 最多也只有4匹马有参赛资格, 只需要一次就可以完赛.
当需要Top4时, 最少需要7次, 最多需要8次
如果继续取Top5, 需要怎么安排.
我们还是首先列出来, 有哪些马有资格争夺前五
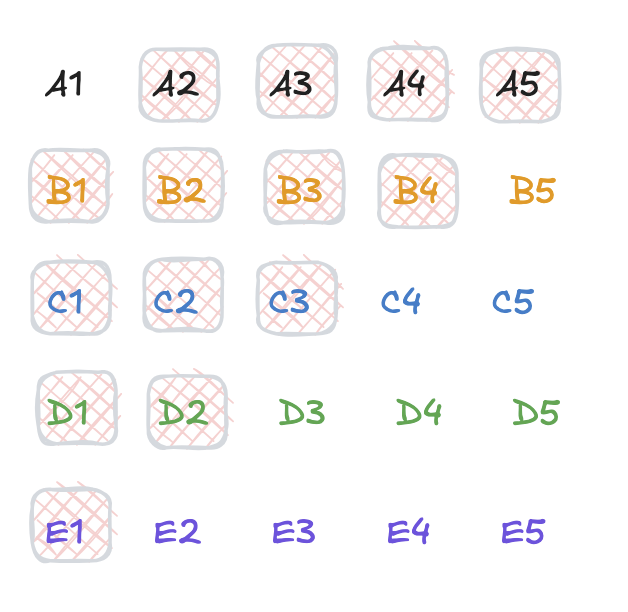 我们按照Top4的经验, 再来看下在已知Top3的情况下, 该如何安排.
我们按照Top4的经验, 再来看下在已知Top3的情况下, 该如何安排.
-
A2, A3是第二, 第三名 此时有资格去与B1, B2, C1争夺前五比赛资格的只有A4,A5而他们正好只有5匹, 正好可以构成一组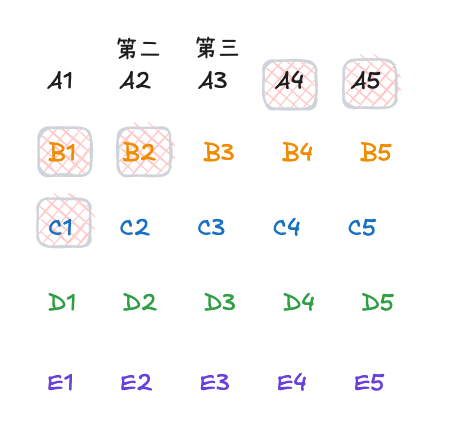
-
A2, B1是二三名 我们假设A2第二,B1第三. 还剩下A3, B2, C1三匹马 如果在第七轮中,A2>B1>A3>B2>C1. 此时A3就是第四名, 第五名的争夺资格只有A4, B2两匹马. 那么如果是A2>B1>B2>A3>C1. 此时仅需对A3, B3进行比赛, 就能找出第五名 如果是A2>B1>C1>A3>B2, 此时抉择第五名就需要C2, D1, A3进行比赛了. 其他情况不再证明, 都是少于5匹马, 可以仅比赛一轮就能完成.
-
B1,B2是二三名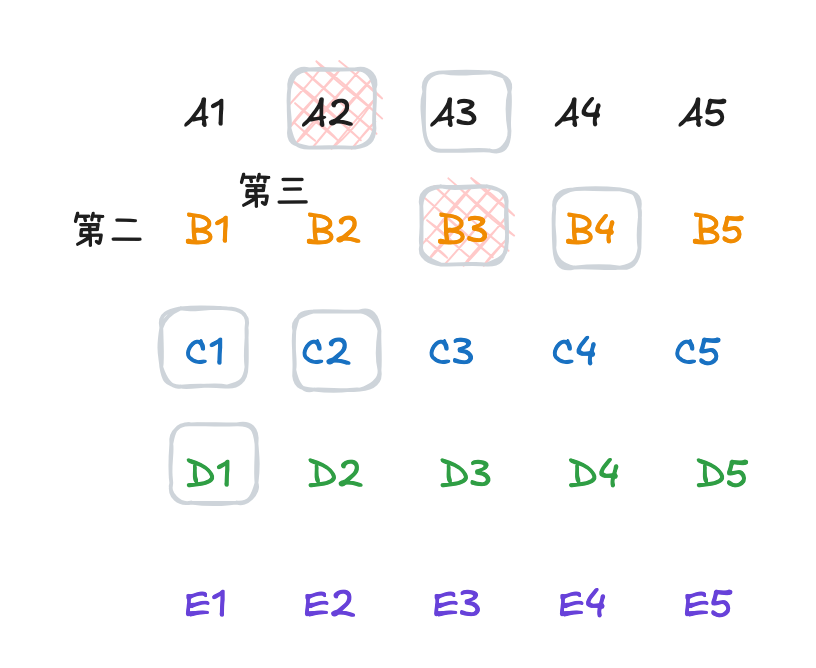 如果在第七轮比赛中,
如果在第七轮比赛中, B1>B2>C1>A2>A3. 此时前五的资格就需要对A2,B3,C2,D1四匹马进行比赛. 也仅需要一轮即可. 其他情况更加简单, 不在讨论. -
B1, C2是二三名 此时是最复杂的情况. 当B1>C2时, 第三名可能是A2或者B2. 但是我们仍然无法确定它是不是全局的第四, 因为没有与D1进行比赛 我们首先进行一轮A2,B2,C2,D1的比赛, 得到第一名. 假如第一名是D1, 此时他是全局第四, 要得到全局第五还需要进行一轮比赛, 让D2,E1与刚刚这一轮的第二名比赛即可 假如第一名是A2/B2/C2任意一名, 则还需要进行一轮A3/B3/C3与第二名的比赛即可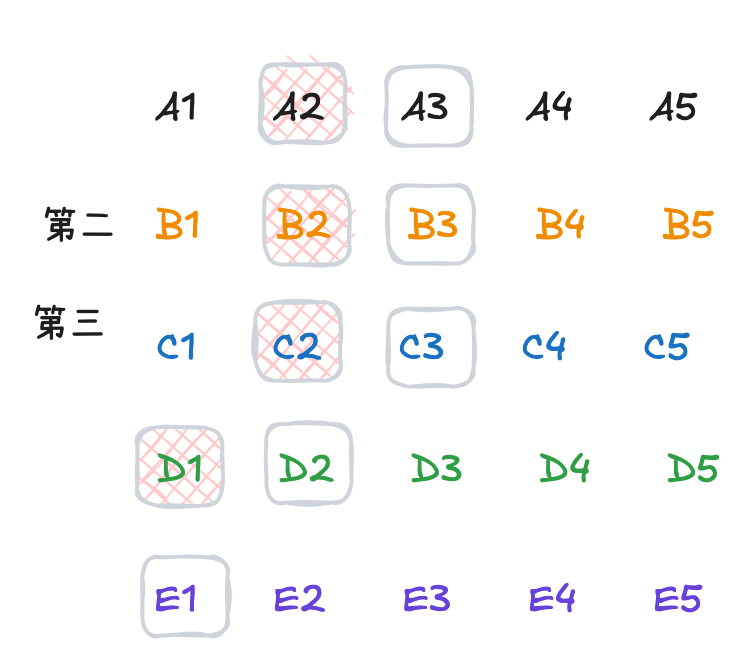
当需要Top5时, 最少是需要8次比赛的. 最多情况下, 进行9次比赛就可以找出top5
总结一下
这道题如果用图的方式来表示, 更加容易理解, 经过前6轮比赛, 可以得到一组关系, 一个根节点, 然后找剩下的最近的4个节点. 每次查找充分利用5条赛道的条件, 得到更多的参数, 从而优化下一次的结果.