最近买了台相机, 出去拍了一些照片, 然后突然想到AI来做照片的处理,优化等. 所以找了一些课程来学习一下图像处理的基础知识. 目前从这些课程中学习: https://www.bilibili.com/video/BV1Kh411X7Qv?p=3 https://www.bilibili.com/video/BV1R84y1f79o?p=1 https://www.bilibili.com/video/BV1tT4y1Y7Ak/?spm_id_from=333.788&vd_source=f7b0753424ba1b445914c36a2cbf1439
基础概念
像素
一张图片在计算机中使用二维数组表示array[m][n]，二维数组的的大小m*n就表示照片的像素
相同的照片尺寸下，一张图片的像素越高，则显示的细节越多。
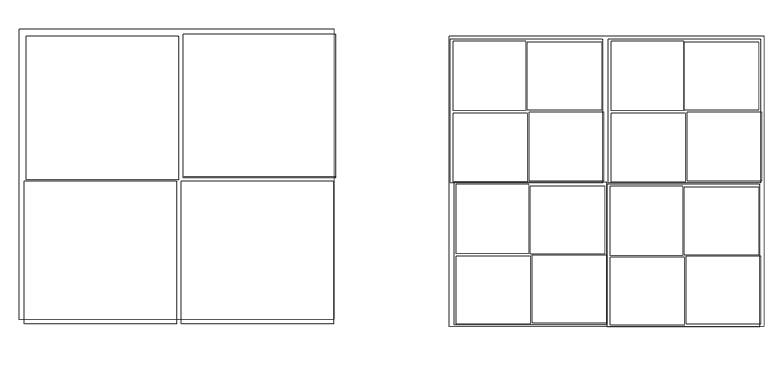
以这个照片为例，左侧图片的像素为2*2，右侧照片像素为4*4, 当放大某个细节时，右侧照片能给出更多的细节。
灰度值
二维数组中填充值的范围，对于黑白照片，灰度值的范围是0-255. 白色为255，黑色为0.
array[m][n]=k, 0<=k<=255
直方图
查看图片中灰度值的分布情况，横坐标是灰度值，纵坐标表示该灰度值出现的频率。
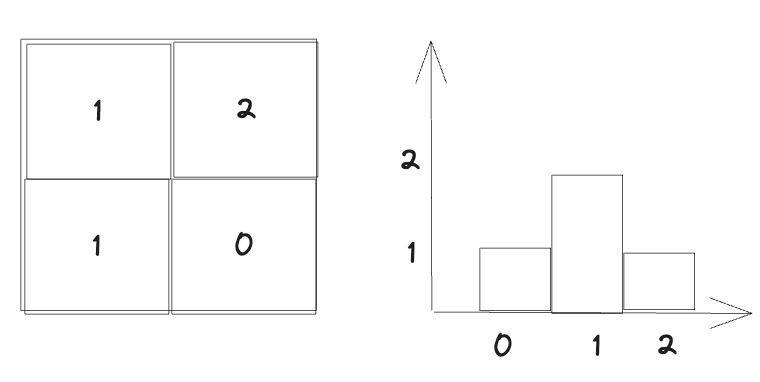要注意的是，一个照片只有一个直方图，但一个直方图并不对应唯一的一张照片
使用直方图可以直观的展示出图像中各个灰度值的分布情况，占比情况。
图像增强
- 灰度变换
- 代数运算
- 空间域滤波
- 频域滤波
灰度变换
- 简单，常用的空间域图像增强方法
- 对输入图像像素的灰度级进行变换 $s=f(r)$, r/s 输入/输出灰度级
f(): 灰度变换函数，这个函数可以是线性变换, 也可以是非线性变换.
线性变换
$s = Ar+B$ 当A>1时, 相当于做灰度拉伸, 变换完的图像会比原来的图片亮. 当A<1时, 相当于做灰度压缩, 变换完的图像会比原来的图片暗.
在线性变换中, 还可以进行分段线性变换 $$ s= \begin{cases} f1(x), \quad 0 <r<a \ f2(x), \quad a\leq r< b \ f3(r), \quad b\leq r< N \end{cases} $$
可以对感兴趣的灰度区域进行突出, 对不感兴趣的灰度区域进行抑制.
非线性变换
对数变换
$s = c * log(1+r)$ 在灰度级比较小(暗)时做拉伸, 在灰度值大(亮)时做压缩, 可以使暗的图像更加亮
幂次变换
$s = c * r^n$ 在n>1时 在灰度值比较大(亮)时做拉伸,在灰度值小(暗)时做压缩 在n<1时 在灰度级比较小(暗)时做拉伸, 在灰度值大(亮)时做压缩
直方图均衡
假设我们使用函数f()来对图像做灰度变换, 那么变换公式为: $D_B=f(D_A), D_A:变换前的灰度值,D_B变换后的灰度值$
我们使用$H(D)$表示灰度直方图, 那么在使用f()做变化之后, 变换后图像的灰度直方图为:
$$H_B(D_B)=\frac{H_A(D_A)}{f\prime(D_A)}$$
灰度变换后图像直方图是:变换前直方图与变化函数导数之比
直方图均衡是希望将图像的
- 每个灰度级都拥有像素
- 直方图分布均匀
如果要达到这个要求, 那么就需要使得
$$H_B(D_B)=\frac{A_0}{D_m} \quad \quad A_0代表图像像素总数,D_m代表灰度级$$
而我们又知道
$$H_B(D_B)=\frac{H_A(D_A)}{f\prime(D_A)}$$
所以我们可以推导出
f()的表达式, 即: $$D_B=f(D_A)=\frac{D_m}{A_0}* \sum_{0}^{D_A}H_A(D_A)$$
代数运算
- 加法运算
- 减法运算
- 乘法运算
加法运算
两幅或多幅图像相加 $C(x,y)=A(x,y)+B(x,y)$
可以用来去除叠加性噪声
减法运算
两幅图像相减 $C(x,y)=A(x,y)-B(x,y)$
可以用来
- 分割特定区域
- 检测场景变化 (通过前后图像相减, 得到变化的值)
乘法运算
两幅图像相乘 $C(x,y)=A(x,y)*B(x,y)$
可以用来获取图像中特点的部分
空间域滤波
$$y(j,i)=\sum_{m}\sum_{n}h(m,n)x(j+m,i+n)$$ 均值滤波器: $$h(m,n) = \left[ \begin{matrix} 1 & 1 & 1 \ 1 & 1 & 1 \ 1 & 1 & 1 \ \end{matrix} \right] * \frac{1}{9} $$ 高斯低通滤波器: $$h(m,n) = \left[ \begin{matrix} 1 & 2 & 1 \ 2 & 4 & 2 \ 1 & 2 & 1 \ \end{matrix} \right] * \frac{1}{16} $$ 可以使图像平滑
中值滤波器 先邻域内像素(包括原像素)灰度排序, 然后取中间值 它可以
- 使突出的点更接近它周边的点
- 消除孤立的亮度或暗点 去除噪声的同时, 比较好的保留边缘 能够有效去除脉冲噪声
高通滤波 使图像锐化
- 突出图像的细节特征
- 增强图像模糊的边缘
- 增强高频
- 突出边缘
一阶
- Robert算子
- Prewitt算子
- Sobel算子 二阶
- Laplace算子
一阶导数可以检测图像中的某像素点是否在边缘上 二阶导数可以判断一个边缘像素点在亮的一侧还是在暗的一侧