题目描述

链接: https://leetcode-cn.com/problems/maximum-sum-circular-subarray/

给定一个长度为n的环形整数数组nums, 返回nums的非空子数组的最大和

环形数组意味着数组的末端和头部是相连的, 所以子数组可以为数组的中间某一段或者首尾两段.

示例1:

输入: nums = [1, -1, 3, -2]

输出: 3

子数组 [3] 为最大和

示例2:

输入: nums = [5, -3, 5]

输出: 10

首尾的子数组[5, 5]得到最大和10

示例3:

输入: [3, -2, 2, -3]

输出: 3

从子数组[3], [3, -2, 2]都可以得到最大和3

解题思路

最大和的子数组有两种情况:

1. 在数组的中间某一段
2. 分别在头尾两端

情况1: 这种情况与非环形数组的解法一致, 对于下标n的位置来说, 当前位置的最大子数组之和为

​ f(n) = Max(f(n-1)+nums[i], nums[i])

再来看情况2: 分别在头尾两端.

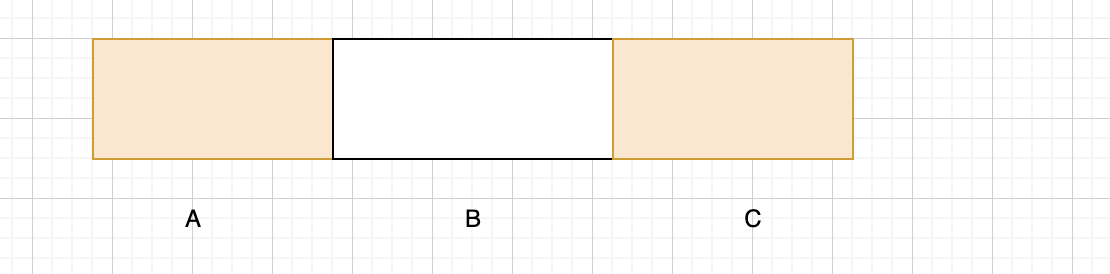
假设我们的子数组由A, C构成.

根据要求可知, A, C组成的子数组为最大子数组的和.

即 MAX(res) = MAX( A+C )

而A+C = SUM-B. 即数组总和减去B

MAX(res) = MAX(A+C) = MAX(SUM-B) = SUM - MIN(B)

由于总和是不变的, 所以我们求A+C的最大值就转化成了求B的最小值

有一种特殊情况需要处理, 即当数组全为负数时, MIN(B) = SUM. 这时不符合题意, 这时的答案应该是MAX(nums)

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

	public static int maxSubarraySumCircular(int[] nums) {
    		int maxFi = 0, minFi = 0, maxAns = nums[0], minAns = nums[0], sum = 0, max = nums[0];
    				for (int num : nums) {
    		    					maxFi = Math.max(maxFi + num, num);
    		    					maxAns = Math.max(maxAns, maxFi);
    		    					minFi = Math.min(minFi + num, num);
    		    					minAns = Math.min(minAns, minFi);
    		    					sum += num;
    		    					max = Math.max(max, num);
		    		}
		    		return Math.max(maxAns, (sum - minAns) == 0 ? max : (sum - minAns));
	}

相关题目