什么是堆

堆是一种特殊的树，它满足以下两点：

堆是一个完全二叉树

完全二叉树要求，除最后一层，其他层的节点个数都是满的，最后一次的节点都靠左排列。
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值

当前节点的值是子树中的最大或最小值。

我们将每个节点的值都大于等于子树中每个节点值的堆，叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”

我们来看一下例子：

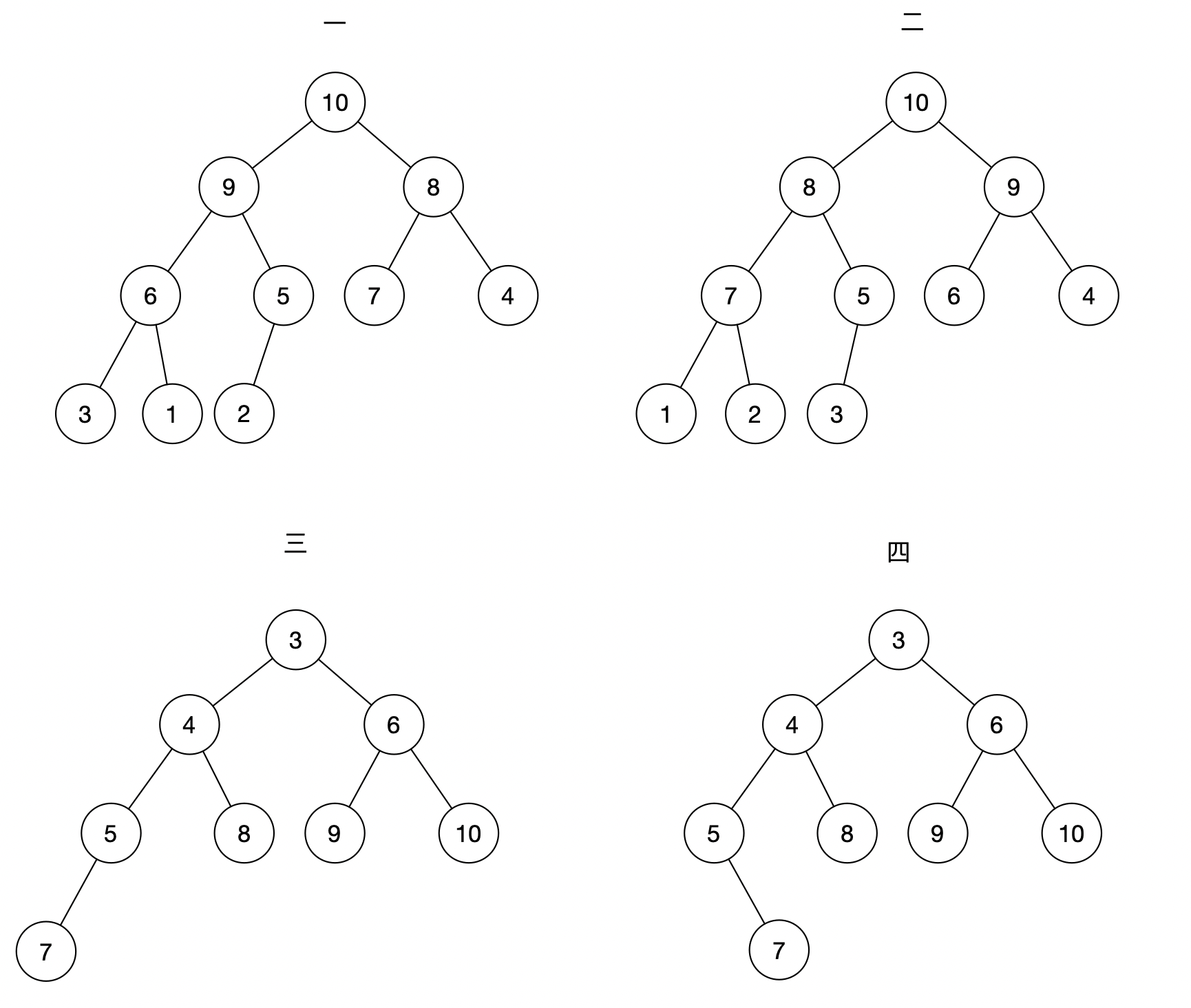
在上面的四个实例中，我们根据以上两条规则，可以判断出：

第一个、第二个是大顶堆，第三个是小顶堆，第四个由于不是完全二叉树所以不是堆。

如何实现一个堆

由于堆是一个完全二叉树，而完全二叉树又适合用数组来存储。

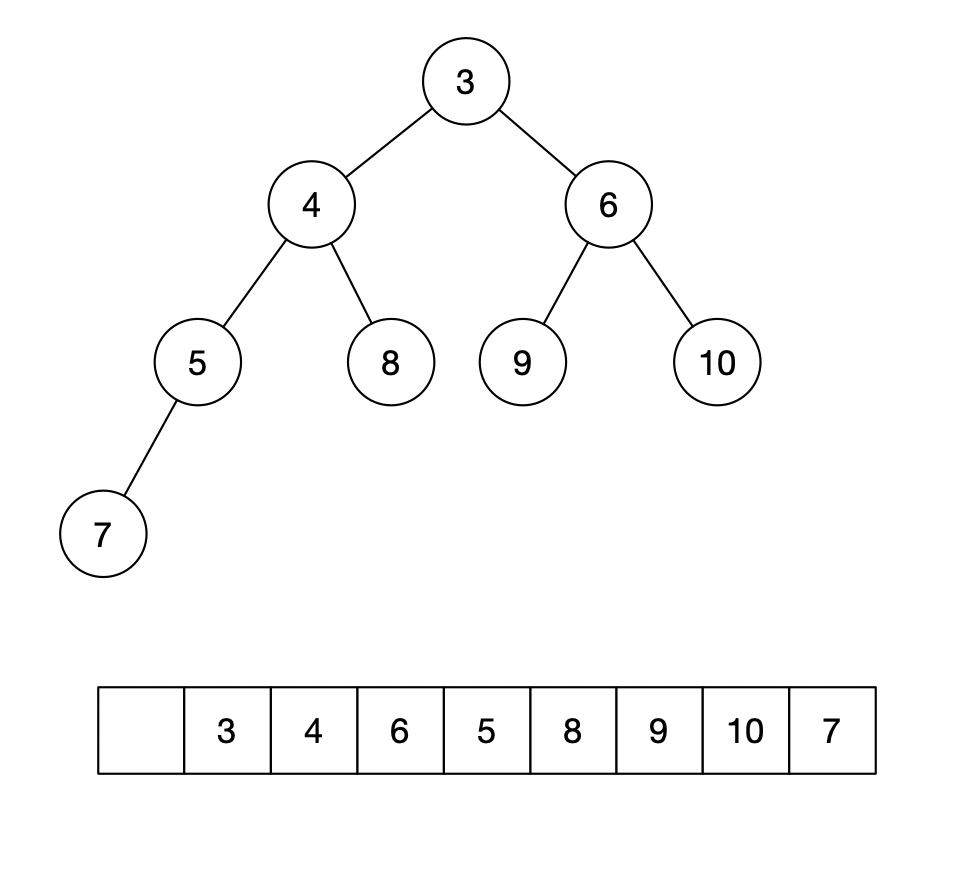
数组下标为i的节点，左子节点是下标为i*2的节点，右子节点是下标i * 2 + 1， 它的父节点是下标为i/2的节点。

对于堆，我们要实现的功能大约有这三个：插入，删除堆顶元素，获取堆内的元素，在这里的实现以大顶堆为例。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


public class Heap {
  
  /**
	 * 数组，从下标1开始存储数据
	 */
  private int[] a;
  
  /**
	 * 堆可以存储的最大数据个数
	 */
	private int n;
  
  /**
	 * 堆中已经存储的数据个数
	 */
  private int count;
  
  /**
	 * 由于使用数组来存储数据，所以需要初始化容量
	 */
  public Heap(int capacity) {
		a = new int[capacity + 1];
    n = capacity;
		count = 0;
	}
  
  /**
	 * 添加元素
	 */
  public void add(int val){
    ...
  }
  
  /**
	 * 删除堆顶元素
	 */
  public void removeTop(){
    ...
  }
  
	/**
	 * 获取堆数据
	 */
  public int[] getHeap(){
    ...
  }
  
}	

获取数据

这个比较简单，我们只要将数组的内容返回即可，但是我们在下标0中没有存储元素，并且可能未填满存在空数据，所以我们可以从1开始复制，复制元素数量的长度。

1
2
3
4
5


public int[] getHeap() {
		int[] r = new int[count];
		System.arraycopy(a, 1, r, 0, count);
		return r;
	}

添加元素

由于我们使用数组，所以存在最大长度，当元素数量未超过最大长度时进行添加，当超过长度后我们需要进行一个策略判断，在这里先直接抛弃。

后面添加元素的时候需要满足堆的规则，就需要进行调整，让其满足堆的特性，这个过程称为堆化。

堆化实际上有两种，从下往上和从上往下。这里使用从下往上的堆化方法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


public void add(int val) {
  if (count >= n) {
    //堆满了，先直接抛弃。
    return;
  }
  addVal(val);
}

private void addVal(int val){
  //堆内元素数量加一
  ++count;
  //将元素放到最后
  a[count] = data;
  int i = count;
  //循环比较当前节点与父节点的大小关系
  //大顶堆时子节点元素要比父节点元素值小。
  while (i / 2 > 0 && a[i] > a[i / 2]) {
    int temp = a[i];
    a[i] = a[i / 2];
    a[i / 2] = temp;
    i = i / 2;
  }
}

删除堆顶元素

根据堆定义规则的第二条可以知道：堆顶元素存储的是堆中数据的最大值或最小值。

我们以上面的大顶堆为例，堆顶元素就是最大值。当需要删除堆顶元素时，就需要第二大的元素放到堆顶，第二个元素就是堆顶元素的子节点。当将第二大元素放到堆顶后，还需要依次填充从子节点添加到父节点的位置，这时虽然完成了删除，但容易出现数组空洞的现象。

以下面这个大顶堆为例：

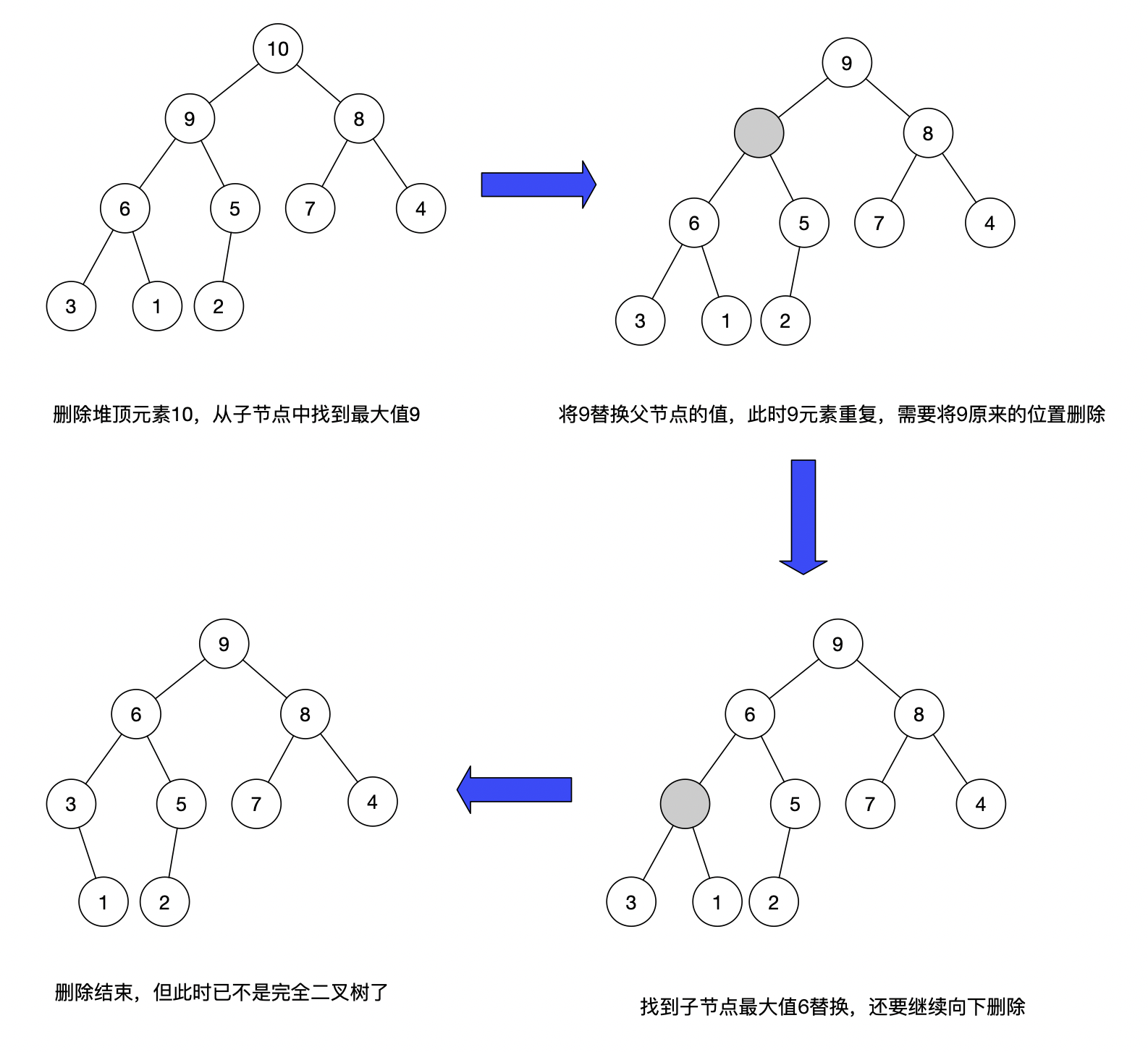
所以这里删除的时候需要转换一下思路：

先将最后一个节点元素放到堆顶，然后再比较父节点于子节点的关系，对于不满足条件的进行替换，直到满足堆的定义为止。这其实是从上往下的堆化方法。

刚才的例子用这个方法再来实现一遍：

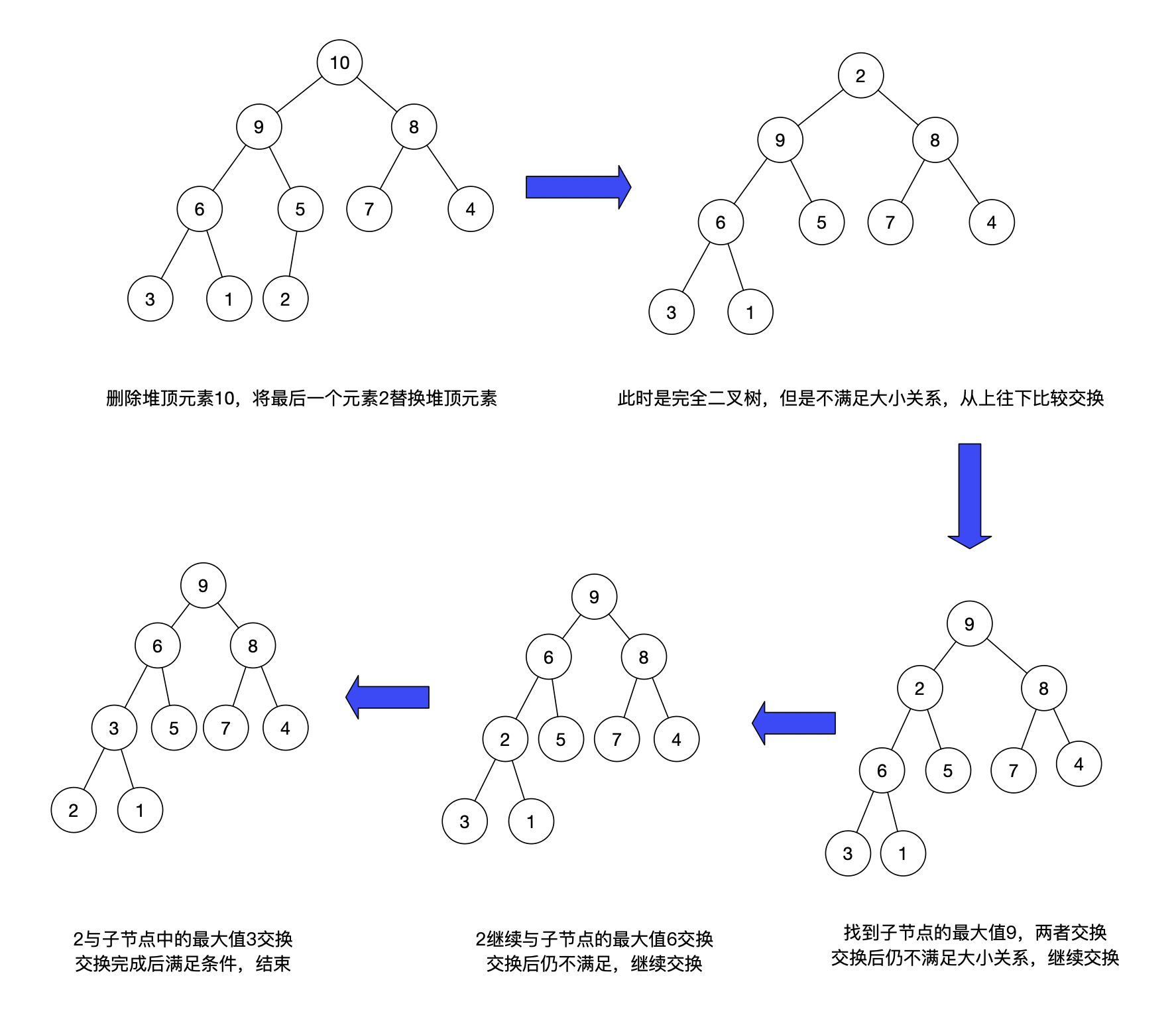
将这个思路转换为代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


public void removeTop() {
  if (count == 0) {
    //堆内没有数据
    return;
  }
  //堆顶元素与最后的元素交换
  a[1] = a[count];
  //数量减少
  --count;
  heapHelp(a, count, 1);
}

//从堆顶开始比较，找到子节点的最大值，然后替换，如果父节点是最大值则终止
private void heapHelp(int[] a, int n, int i) {
  while (true) {
    		//当前节点的数据可能比子节点的数据大，所以与两个子节点对比，找到最大值后进行替换
				int maxPos = i;
				//需要注意不能下标越界
				if (i * 2 <= n && a[i] < a[i * 2]) {
					maxPos = i * 2;
				}
				//先判断左子节点，然后判断左子节点与右子节点的大小
				if (i * 2 + 1 <= n && a[maxPos] < a[i * 2 + 1]) {
					maxPos = i * 2 + 1;
				}
				if (maxPos == i) {
					//如果父节点比两个子节点都大，则不需要替换，满足条件退出
					break;
				}
				//将父节点与最大子节点进行替换
				int temp = a[i];
				a[i] = a[maxPos];
				a[maxPos] = temp;
				//然后递归判断子节点是否满足条件，直到满足条件后退出
				i = maxPos;
  }
}

至此就完成了大顶堆的数据访问，添加元素，删除堆顶元素操作。

这里实现的是大顶堆，如果实现小顶堆，只要比较条件中进行一些更改即可完成。

在这里的添加元素，当超过数量时直接进行了抛弃，对于一些应用不符合，这一部分放在应用练习中进行操作。

堆排序

从上面的几个例子可以看出，拿到存放堆的数组遍历后的数据并不是有序的。所以不能直接返回堆数组。

由于堆顶元素是最大值，所以我们可以将最大值与最后一个元素n进行交换，然后对前面的n-1个元素重新建堆。堆化完成后再取堆顶元素，放到n-1的位置，依次进行交换，堆化的过程，直至结束。

用下面的图来看一下流程：

用代码来实现一下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


/**
* 堆排序
* 如果要对[19,4,6,3,22,8,7]这个数组排序，首先要将数组长度加一，首位补零
* 改成这样的结构:[0,19,4,6,3,22,8,7]
* 然后调用此函数时，参数为 heapSort(a,a.length-1)。
* 总之，传入长度应为数组长度减一，则会对除首位的其他元素排序
*
* @param a 数组
* @param n 要排序的长度
*/
public void heapSort(int[] a, int n) {
  //首先按照大顶堆建堆，完成后第一个元素就是最大的元素
  buildHeap(a, 10);
  int k = n;
  while (k > 1) {
    //将最大的元素，即1，与最后一个元素交换，那最大元素就放到了下标为n的位置
    swap(a, 1, k);
    --k;
    //然后重新建堆，将剩下的n-1个元素重新构建成堆，再继续交换
    heapHelp(a, k, 1);
  }
}

/**
* 建堆
* 按照大顶堆来完成，即每个元素都比下面的元素大
*
* @param a 数组
* @param n
*/
private void buildHeap(int[] a, int n) {
  for (int i = n / 2; i >= 1; --i) {
    heapHelp(a, n, i);
  }
}

/**
* 建堆
*
* @param a
* @param n
* @param i
*/
private void heapHelp(int[] a, int n, int i) {
  while (true) {
    int maxPos = i;
    if (i * 2 <= n && a[i] < a[i * 2]) {
      maxPos = i * 2;
    }
    if (i * 2 + 1 <= n && a[maxPos] < a[i * 2 + 1]) {
      maxPos = i * 2 + 1;
    }
    if (maxPos == i) {
      break;
    }
    swap(a, i, maxPos);
    i = maxPos;
  }
}

这个实现中需要注意一点，即由于堆的特性，下标0不存储元素，所以我们这里只会除首位外的元素排序。也可以再封装一层再操作。

习题

最小的k个数

参考：

数据结构与算法之美

堆以及堆排序

什么是堆

如何实现一个堆

获取数据

添加元素

删除堆顶元素

堆排序

习题

参考：